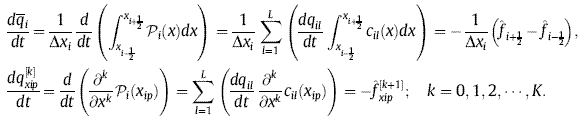A new high-order finite volume method based on local reconstruction is presented in this paper. The method, so-called the multi-moment constrained finite volume (MCV) method, uses the point values defined within single cell at equally spaced points as the model variables (or unknowns). The time evolution equations used to update the unknowns are derived from a set of constraint conditions imposed on multi kinds of moments, i.e. the cell-averaged value and the point-wise value of the state variable and its derivatives. The finite volume constraint on the cell-average guarantees the numerical conservativeness of the method. Most constraint conditions are imposed on the cell boundaries, where the numerical flux and its derivatives are solved as general Riemann problems. A multi-moment constrained Lagrange interpolation reconstruction for the demanded order of accuracy is constructed over single cell and converts the evolution equations of the moments to those of the unknowns. The presented method provides a general framework to construct efficient schemes of high orders. The basic formulations for hyperbolic conservation laws in 1- and 2D structured grids are detailed with the numerical results of widely used benchmark tests.

This paper was published as: 

 Ii S, Xiao F. High order multi-moment constrained finite volume method.  Part I: Basic formulation. Journal of Computational Physics,228(10):3669-3707(2009)