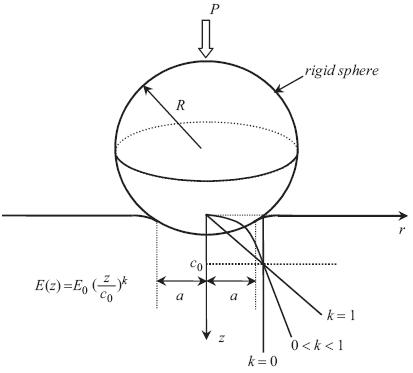
We consider adhesive contact between a rigid sphere of radius R and a graded elastic half-space with Young's modulus varying with depth according to a power law E = E-0(z/c(0))(k) (0 < k < 1) while Poisson's ratio v remaining a constant. Closed-form analytical solutions are established for the critical force, the critical radius of contact area and the critical interfacial stress at pull-off. We highlight that the pull-off force has a simple solution of P-cr= -(k+3)pi R Delta gamma/2 where Delta gamma is the work of adhesion and make further discussions with respect to three interesting limits: the classical JKR solution when k = 0, the Gibson solid when k --> 1 and v = 0.5, and the strength limit in which the interfacial stress reaches the theoretical strength of adhesion at pull-off.
This paper was published as:
Chen SH, Yan C, Zhang P, Gao HJ. Mechanics of adhesive contact on a power-law graded elastic half-space. Journal of the Mechanics and Physics of Solids,57(9):1437-1448(2009)