Shear banding as the basic deformation mode is considered the culprit behind unpredictable and often catastrophic failure of a variety of amorphous solids. In history, there are two classical languages to describe the shear banding mechanism in amorphous solids: one is local coalescence of free volume, i.e., the so-called Reynolds dilatancy, and the other is nonlocal effect of shear-transformation (ST)-type rearrangements of constituent atoms or particles.
Recently, researchers from the Institute of Mechanics of the Chinese Academy of Sciences, Dalian Jiaotong University, etc. have united the two classical mechanisms through quantitatively clarifying the causality between STs and dilatation in shear banding instability.
Related results were published in Physical Review E.
The researchers used a real 3D colloidal glass under simple shear as proof of principle. This amorphous solid displayed the homogeneous deformation at low strain rates and the shear-banded inhomogeneous flow at strain rates higher than the inverse structural relaxation time. They calculated the spatial autocorrelation of both shear strain and free volume at the particle level, which characterizes with fidelity the elastic shear and dilatation fields induced by STs, respectively.
Results showed that accompanying the emergent shear banding, the elastic response fields of the system, typical of a quadrupole for shear and a centrosymmetry for dilatation, lose the Eshelby-type spatial symmetry; instead a strong correlation appears preferentially along the banding direction.
By quantifying the fields’ spatial decay, they identified an elastic criterion for the shear banding instability, that is, the strongly-correlated length of dilatation is smaller than the full length of shear correlation. Specifically, ST-induced free volume has to be confined within the elastic shear domain of ST so that those STs could self-organize to trigger shear banding. This physical picture is directly visualized by tracing the real-space evolution of local dilatation and ST-particles.
These findings coordinate local effect of free volume with nonlocal effect of STs, and provide the first experimental evidence for the STs’ avalanche into shear banding in amorphous solids.

Elastic shear (left) and dilatation (right) fields for homogenous deformation (upper) and shear banding (lower) in the colloidal glass
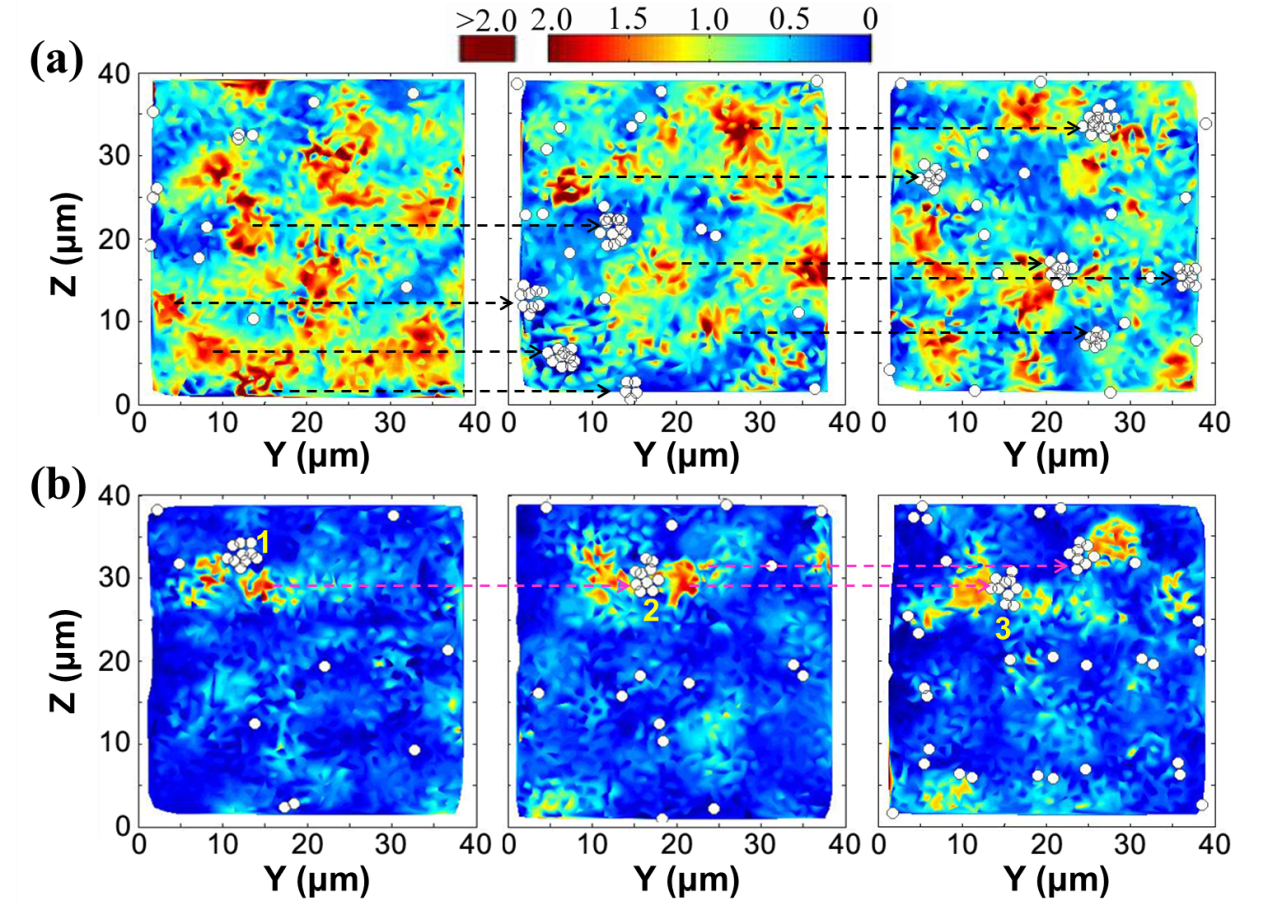
The real-space trace of local dilatation and ST-particles for homogenous deformation (a) and shear banding (b)