Determination of the microstructure of materials is the premise of understanding and modifying materials. The term ‘chemical-disordered materials’ stems from the semi-ordered materials whose lattice is periodic (thus crystal) but the occupying atom species are non-periodic in space. From the point view of chemical compositions, the chemical-disordered materials can be classified into anionic, cationic, and defected counterparts, which can be simply considered as the anions, cations and defects occupy the non-periodic sites. Chemical-disordered materials are widely used in many areas including semiconductors, high-temperature superconductors, Li-ion batteries, metal alloys, ceramics, and heterogeneous catalysts due to their special properties and performances. It is very important to study the structure of disordered materials for understanding the properties of disordered materials and guiding experiments. The exact structure of chemical-disordered materials has not been solved because of the uncertainty of atomic occupancy at some lattice sites. Structural prediction of chemically disordered materials is challenging and becomes more complex with increasing system size. Previous studies have used techniques such as crystal symmetry, cluster expansion and machine learning potential to accelerate structural prediction of chemically disordered materials, but still face a large number of expensive first-principles calculations.
Researchers from Institute of Mechanics, CAS, and Institute of Coal Chemistry, CAS/Synfuels China Technology Co. Ltd, developed the LAsou method for highly efficient structure prediction of chemical-disordered materials. Tests on three different typical finite-size systems, which included the anion-disordered BaSc(OxF1?x)3 (x=0.667), the cation-disordered Ca1?xMnxCO3 (x=0.25), and the defect-disordered ε-FeCx (x=0.5) show that the LAsou method can quickly find thermodynamically stable structures with much less (serval orders of magnitude) first-principles calculations compared to traditional enumeration methods. These demonstrations confirm that the LAsou method is a simple yet highly efficient approach that combines the first-principles calculations and active-learning algorithm to search for the thermodynamically stable structures of chemical-disordered materials, which shows great potential to solve the ‘exponential-wall’ problem for many-body systems. In LAsou method, the ML potential can largely reduce the DFT calculations via predicting and filtering from the large sampling space, the ensemble learning algorithm can significantly improve the stabilities for the prediction of energy and relaxation, and the active learning algorithm can gradually improve the accuracy of ML potential on-the-fly so that one doesn’t have to pre-prepare a large amount of training data. With these advantages and features, the LAsou method will be helpful for a wide range of applications for the larger, more complex, quasi-infinite size systems and the new materials that occurs in nanoparticles, catalysts, solid solutions, high-entropy alloys and high-entropy oxides, and so on.
This article entitled “Active learning to overcome exponential-wall problem for effective structure prediction of chemical-disordered materials” was recently published in npj Computational Materials 9, 12 (2023)。Xiao-dong Wen and Yu-Wei Zhou from Institute of Coal Chemistry, CAS/Synfuels China Technology Co. Ltd, and Qing Peng from Institute of Mechanics, CAS are co-corresponding authors, and Xiao-ze Yuan from Institute of Mechanics is the first author. This work is supported by the National Key R&D Program of China and LiYing Program of the Institute of Mechanics, Chinese Academy of Sciences.
Original article link:https://doi.org/10.1038/s41524-023-00967-z
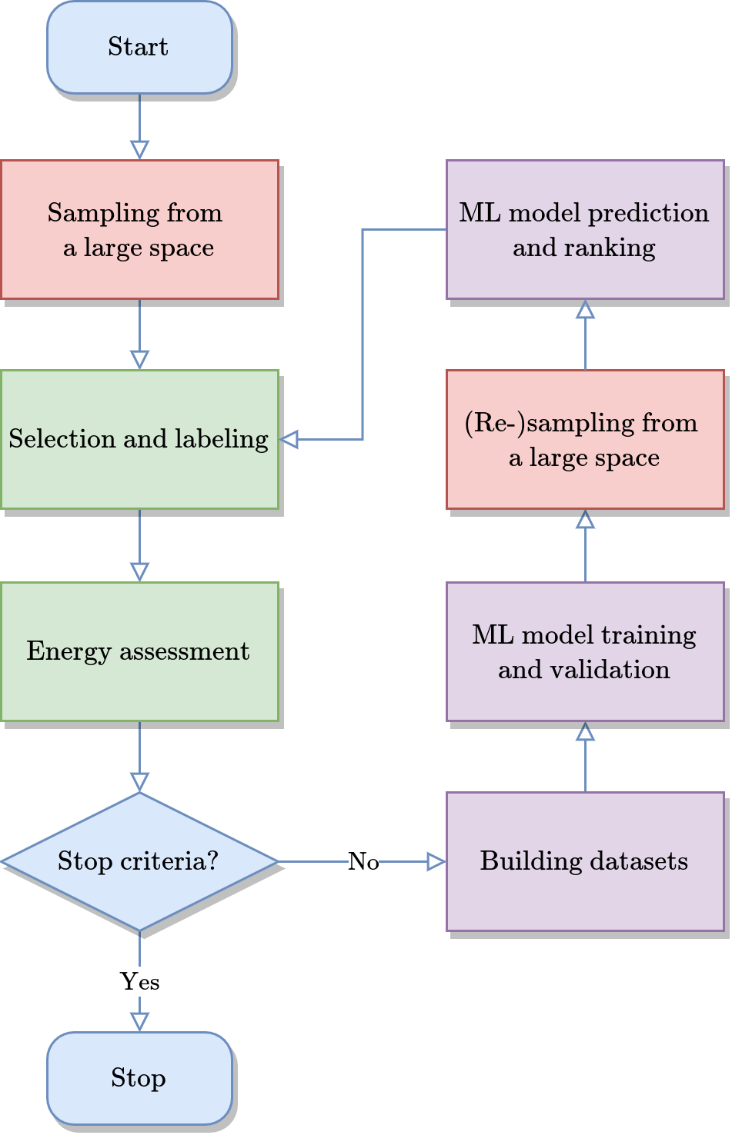
Figure. 1 Flowchart of the active learning-based LAsou method. An overview of the proposed approach for the structure prediction of finite-sized chemical-disordered materials coupled with first-principles calculations.
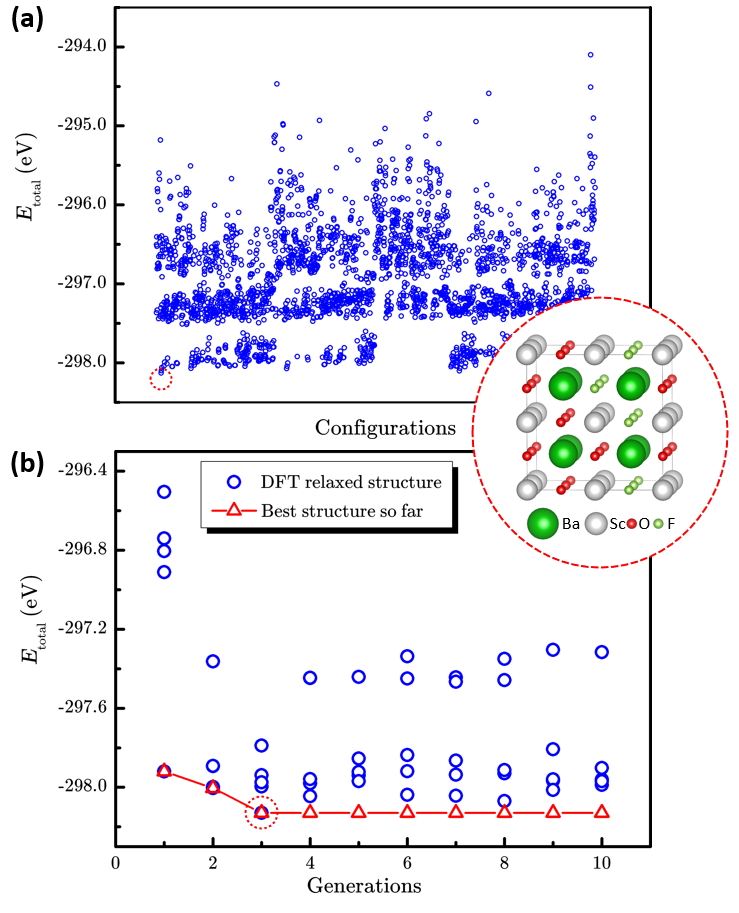
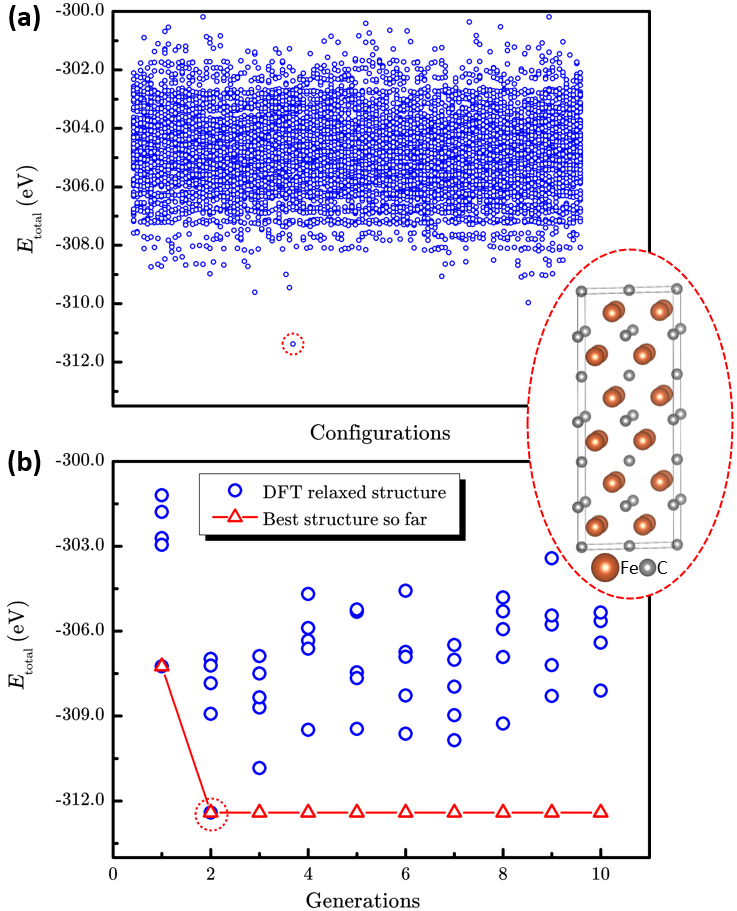
Figure 2. The performance of enumeration method and LAsou method for BaSc(OxF1?x)3(x=0.667).a The scatter plot of total energy of 2664 enumerated structures and the most stable structure. (The blue circles represent the energy for each structure, the red dashed circle represents the best structure with lowest energy.) b The searching process of LAsou method for the total DFT energy against with generation. (The red triangles represent the lowest energy structures searched in history.)
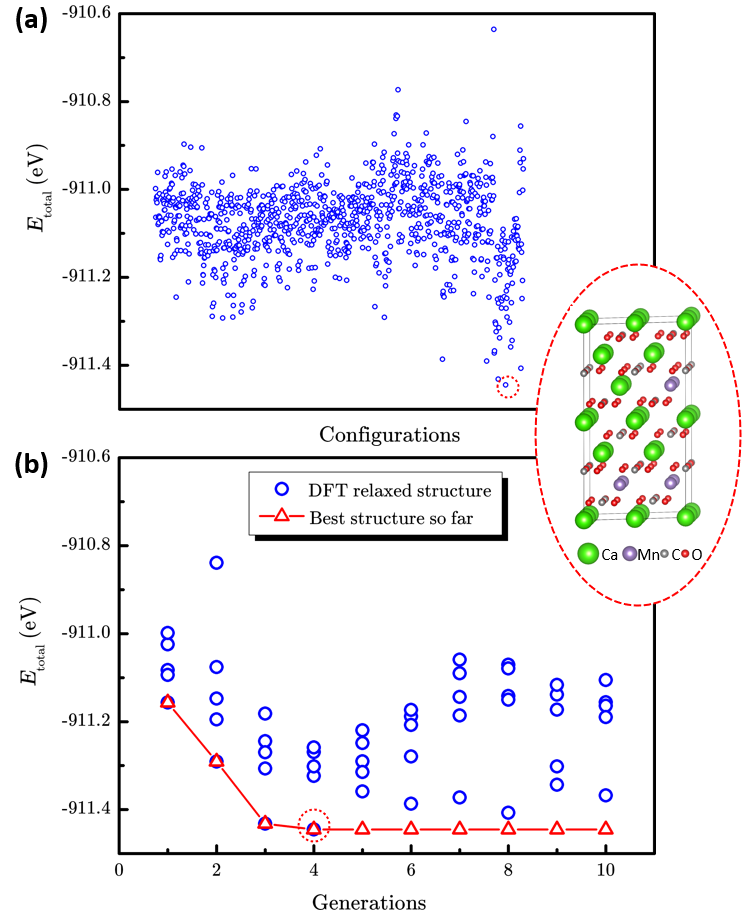
Figure 3. The performance of enumeration method and LAsou method for Ca1?xMnxCO3 (x=0.25). a The scatter plot of total energy of 1033 enumerated structures and the most stable structure. b The searching process of LAsou method for the total DFT energy against with generation.