Researchers from Micro/nanofluidics Group at Institute of Mechanics, Chinese Academy of Sciences (CAS) studied single-particle dynamics in a low-Reynolds-number fluid under spherical confinement using high-performance computers (Fig. 1). Particle motion under the external force in a stationary cavity was analyzed first. When the force is parallel or transverse to the particle-cavity line of centres, they obtained hydrodynamic mobilities of spherical, prolate, and oblate particles. The mobilities show maximum in the cavity centre and decay as the particle moves towards the no-slip wall. Due to particle anisotropy, mobilities of prolate and oblate spheroids are also related to the angle between the particle's axis of revolution and the particle-cavity line of centres.
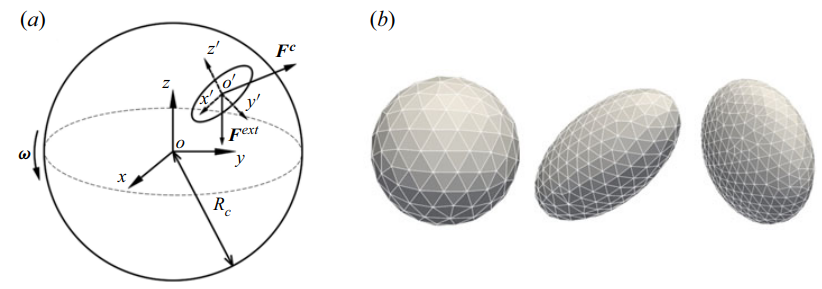
Figure 1 (a) Schematic of the simulation system for studying single-particle dynamics in a low-Reynolds-number fluid confined by a spherical cavity; (b) Discretizations of the sphere, prolate spheroid and oblate spheroid considered in this work.
When the external force is not parallel or transverse to the particle-cavity line of centres, the particle also exhibit motion (drift) transverse to the external force (Fig. 2a). It was found that the drift is caused by the confinement-induced anisotropy of the mobility in the cavity. In the symmetry plane of the cavity, drift velocity of the spherical particle exhibit diagonal symmetry (Fig. 2b). When the particle is near the cavity centre (wall), the drift velocity increases (decreases) as the particle radial position increases; as the particle-to-cavity size ratio increases, normalized drift velocity at a certain position becomes larger (Fig. 2c). Drift velocities of prolate and oblate spheroids is a sinusoidal function of particle orientation.
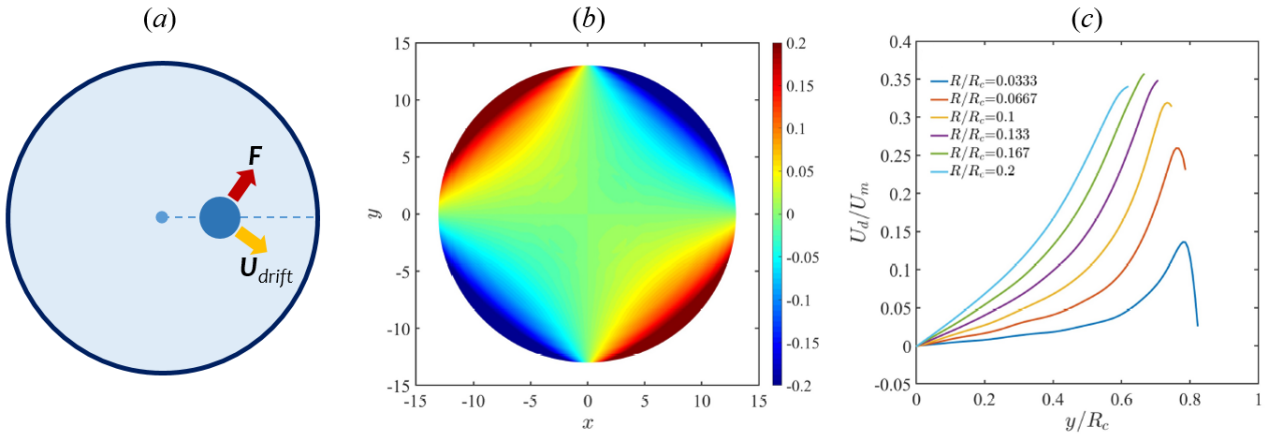
Figure 2 (a) Particle under the external force (red arrow) in the cavity can exhibit a drift motion (yellow arrow); (b) Two-dimensional distribution of the spherical particle's drift velocity on the symmetry plane in the cavity; (c) Normalized drift velocity of the spherical particle with different particle-to-cavity size ratios plotted against the scaled particle position in y-direction when x=?Rc/2. Here Ud and Um are drift and main velocities, respectively.
In many applications, droplets and cells can exhibit both translational and rotational motion. The rotational motion can induce a rotating flow in the cavity. Therefore, particle dynamics in a rotating cavity was investigated. When the particle density is larger (smaller) than fluid density, the particle is under a centrifugal (centripetal) force in the rotating flow. Results showed that, if the particle is released from any position in the cavity, the particle under centrifugal force will eventually move into a stable orbit in the symmetry plane of the cavity, and exhibit periodic motion thereafter (Fig. 3a); the particle under the centripetal force will eventually arrive at the same stagnation point (Fig. 3b). This finding also provides a new strategy to focus and separate particles with different densities in microdroplets or microcapsules.
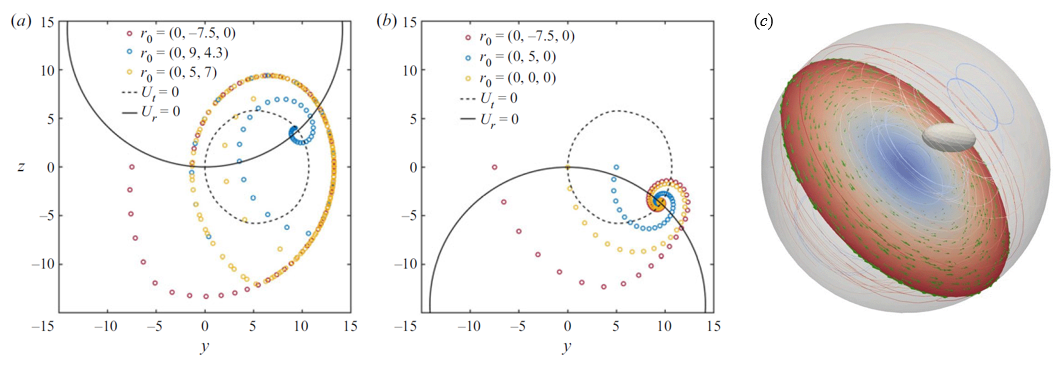
Figure 3 Trajectories of the particle under centrifugal (a) and centripetal (b) forces in the rotating cavity; (c) Snapshot of the prolate spheroid in the rotating flow.
Different from the spherical particle, the rotating flow can induce a torque on the ellipsoidal particle (Fig. 3c), and this torque can alter particle orientation during its motion in the flow. Through mathematical derivation, analytical expressions for the torque on general ellipsoids were obtained, and it was found that the torque is related to the angular velocity of the rotating flow, the difference between particle and fluid densities, and sizes of the ellipsoid’s principle axes. Further research revealed that, under the influence of the rotation-induced torque, there exists different stable and metastable states for the orientations of prolate and oblate spheroids. These states depend on particle shape and rotation-induced torque.
Results from this work form the basis for studying more complex dynamics of spherical and non-spherical particles under total confinements. Transport phenomena and mechanisms revealed here can be useful for understanding intracellular transport and improving microfluidic applications such as encapsulation technologies and droplet-based microreactors. The above results were published in Journal of Fluid Mechanics, and the first author is Master Student Gaofeng Chen (Fig. 4). This work was supported by the Young Elite Scientists Sponsorship Program by the Chinese Society of Theoretical and Applied Mechanics, and by a grant from CAS (no. 025GJHZ2022023MI).

Figure 4 A snapshot of the article.