Professor Ya-Pu Zhao's team at the Institute of Mechanics, Chinese Academy of Sciences, has developed a ground-breaking hyperelastic constitutive relation for soft elastomers with thermally-induced residual stress. The relation is based on Riemann geometry. Their paper, titled “Hyperelastic constitutive relations for soft elastomers with thermally-induced residual stress”, has been published in the prestigious International Journal of Engineering Science. Weiting Chen, a PhD student at the Institute of Mechanics, Chinese Academy of Sciences, is the first author of the paper and Professor Ya-Pu Zhao is the corresponding author.
According to the previously established framework based on Riemannian geometry “Chen, W.T., Zhao, Y.-P., 2022. Thermo-mechanically coupled constitutive equations for soft elastomers with arbitrary initial states. Int. J. Eng. Sci. 178, 103730”, an inhomogeneous free thermal expansion can be induced to compensate for the incompatibility or, more explicitly, the Riemannian curvature brought about by the isothermal release of the given initial stress. On this basis, this study considers material Riemann connections. A compatibility-broken curvature compensation (CBCC) framework based on finite thermoelasticity is established. Such a mechanism indicates the non-local effect of the initial stress, which fundamentally modifies the traditional view that invariant formulations cover all possible functional dependence of the initial stress. More importantly, the governing equations obtained are similar to Einstein's field equation of general relativity. This similarity may deeply imply a standard mechanism concerning the curvature compensation leading to initial stress generation. It opens a new perspective to understand the nature and effects of initial stress and can be extended to other origins of initial stress that have a curvature compensation mechanism.
Links to the papers:
https://doi.org/10.1016/j.ijengsci.2023.103991
https://doi.org/10.1016/j.ijengsci.2022.103730

Figure 1. Diagrammatic sketch of the compatibility-broken curvature compensation framework. (a) Conventional thermoelasticity. (b) The current constitutive theory.
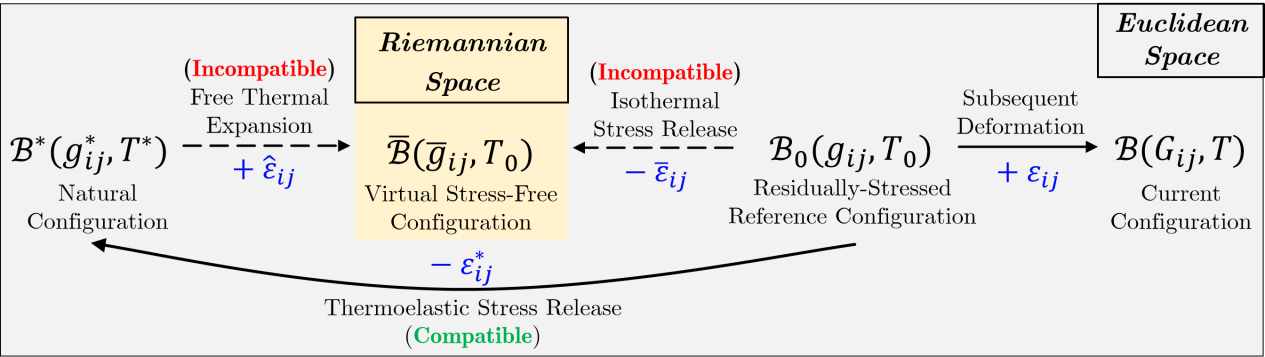
Figure 2. The decomposition of material strains and the associated compatibility-broken curvature compensation framework.