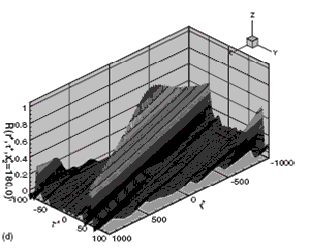
Space-time correlations or Eulerian two-point two-time correlations of fluctuating velocities are analytically and numerically investigated in turbulent shear flows. An elliptic model for the space-time correlations in the inertial range is developed from the similarity assumptions on the isocorrelation contours: they share a uniform preference direction and a constant aspect ratio. The similarity assumptions are justified using the Kolmogorov similarity hypotheses and verified using the direct numerical simulation (DNS) of turbulent channel flows. The model relates the space-time correlations to the space correlations via the convection and sweeping characteristic velocities. The analytical expressions for the convection and sweeping velocities are derived from the Navier-Stokes equations for homogeneous turbulent shear flows, where the convection velocity is represented by the mean velocity and the sweeping velocity is the sum of the random sweeping velocity and the shear-induced velocity. This suggests that unlike Taylor's model where the convection velocity is dominating and Kraichnan and Tennekes' model where the random sweeping velocity is dominating, the decorrelation time scales of the space-time correlations in turbulent shear flows are determined by the convection velocity, the random sweeping velocity, and the shear-induced velocity. This model predicts a universal form of the space-time correlations with the two characteristic velocities. The DNS of turbulent channel flows supports the prediction: the correlation functions exhibit a fair good collapse, when plotted against the normalized space and time separations defined by the elliptic model.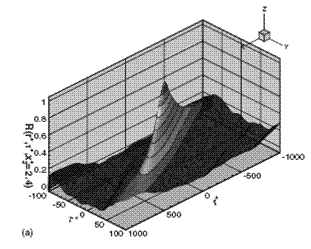
This paper was published as:
Zhao X, He GW. Space-time correlations of fluctuating velocities in turbulent shear flows. Physical Review E,79(4):046316(2009)