The challenges addressed in this work center around the improvement of the existing Chaboche constitutive model to accurately characterize relaxation phenomena under different loading cycles and durations. During high-temperature relaxation processes, dislocations in structural metal materials undergo static recovery, leading to a decrease in dislocation density and a corresponding reduction in stress levels. In the classical Chaboche model, the static recovery term is employed to describe stress relaxation phenomena. However, as the parameters of the static recovery term are constants, the classical Chaboche model fails to accurately capture the relationship between stress relaxation and the number of loading cycles. To address this issue, previous researchers transformed the parameters of the static recovery term into a function of accumulated plastic strain to better depict the changing relationship of stress relaxation. Nevertheless, even with this enhancement, the modified constitutive model still struggled to effectively describe relaxation phenomena over long cycles. To overcome this challenge, the present study introduces a constitutive model incorporating the time factor.

(1) Model Improvement. Building upon the physical deformation mechanisms based on the relaxation process, we enhanced the static recovery term in the kinematic hardening equation by incorporating the influence of time. The stress relaxation and static recovery in metal materials at high temperatures are closely linked, with the primary physical mechanisms involving the migration of dislocations and the slip of thermally activated dislocations. From a dynamic perspective, the evolution during the dislocation relaxation process is not only dependent on the initial dislocation density but also correlated with the evolution time. Therefore, in terms of macroscopic mechanical response, the relaxation stress is related not only to the accumulated plastic strain but also to time. Based on this understanding, we configured the parameters of the static recovery term as a function of accumulated plastic strain and relaxation time. This enhancement more accurately reflects the stress relaxation behavior of metal materials at high temperatures, thereby improving the predictability and applicability of the model.

(2) In the constitutive model, the calibration of parameters related to static recovery typically involves the conventional "trial-and-error" method. However, our constitutive model involves multiple parameters related to static recovery, and these parameters are interrelated, rendering the traditional trial-and-error method inadequate for calibration. Consequently, we introduced a machine learning approach within the framework of Bayesian inversion. By leveraging the results of cyclic stress relaxation and long-term stress relaxation experiments, we successfully obtained the corresponding parameter values. As illustrated in Figure 1, the parameter values obtained through Bayesian inversion demonstrate exceptional capability in describing stress relaxation responses under different cycle counts and long cycles. This method enables us to more accurately determine model parameters, thereby enhancing the accuracy and applicability of the model.

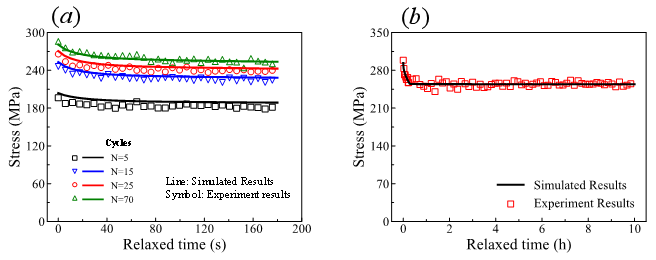
Figure 1: comparison between numerical and experimental results: (a) relaxation curves for different cycle counts under cyclic loading; (b) long-term relaxation curve after 200 cycles of low-cycle fatigue.

To validate the applicability of our constitutive model in "inelastic assessment," we compared the numerical results of the model under multiaxial loading conditions with experimental results. As depicted in Figure 2, we conducted a comparison using notched specimens under complex loading paths, while Figure 3 presents comparative results for rod materials under tension and torsion loading. It is evident that our developed constitutive model accurately captures the high-temperature deformation behavior of materials under multiaxial stress states.