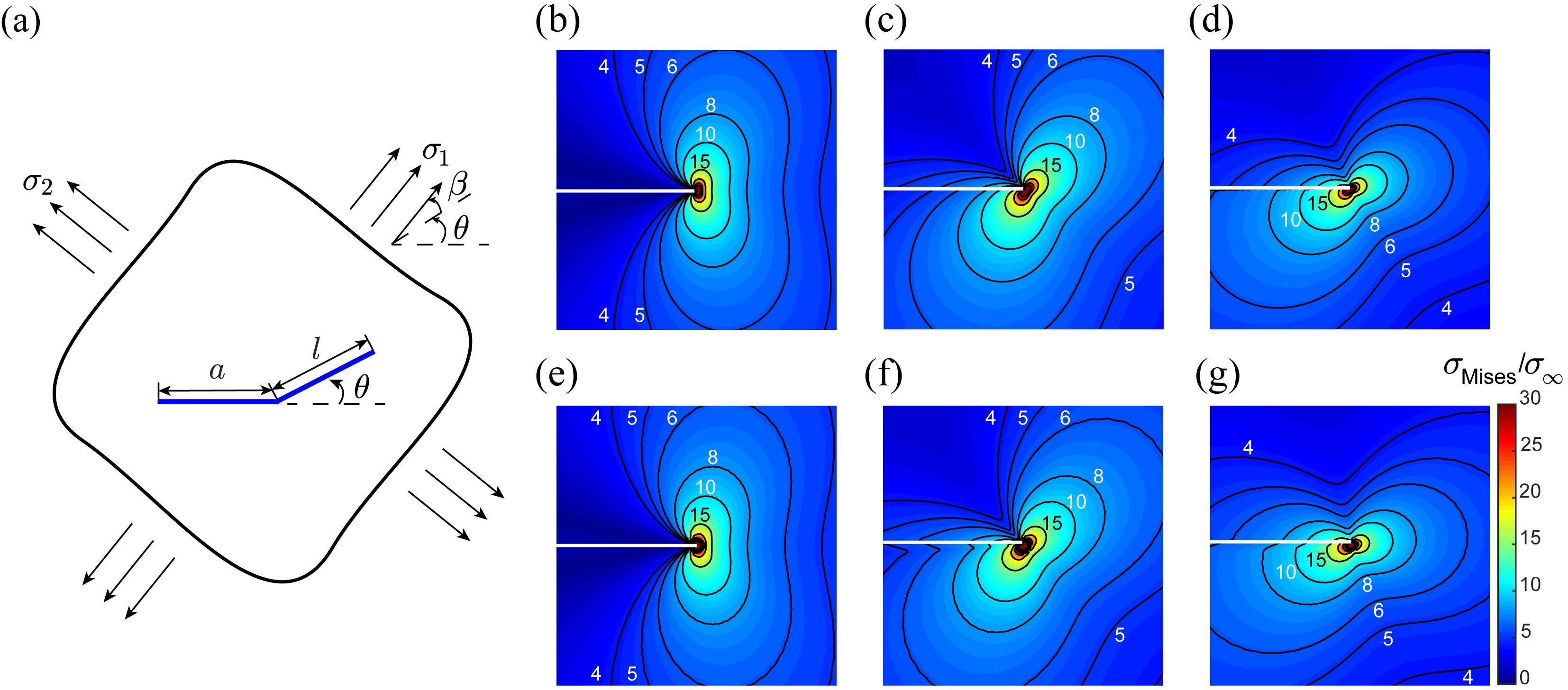
Crack deflection is inevitable in engineering practice, and it is also one of the most classic problem in fracture mechanics. Cracks may deflect due to dynamic instability, running into pre-existing weak regions of heterogenous media, or encountering variation in driving forces. After years of attempts, researchers from LNM, Institute of Mechanics, Chinese Academy of Sciences made a breakthrough in the analytical solutions of stress fields to kinked cracks. This research is published recently on Journal of the Mechanics and Physics of Solids in the title “An analytical solution to the stress fields of kinked crack” (https://doi.org/10.1016/j.jmps.2021.104619).

By employing Schwartz-Christoffel mapping and Muskhelishvili approach, the researchers obtained the analytical complex potentials of the corresponding elastic problem. Based on this they calculated the elastic stress fields of a kinked crack with an arbitrary size (seeing Fig. 1 the comparison of theoretical and numerical methods). The former methods based on perturbation method and superposition of T-stress proposed by the leading scientists in fracture mechanics James Rice and John Hutchinsion, respectively, are only applicable in slightly kinked cracks. This research broke through the limitation of size of kinked length, and established a framework for obtain the stress fields of an arbitrary sized kinked crack. This framework can be extended to multiple-kinked cracks and provide a tool to deeply understand the deflection of cracks and the formation of crack networks.

The first author of this paper is Zhuo-Er Liu, Ph. D. students in Institute of Mechanics, CAS, and the corresponding author is Professor Yujie Wei. This research is supported by the NSFC Basic Science Center for “Multiscale Problems in Nonlinear Mechanics” (No. 11988102) and the strategic Priority Research Program of the Chinese Academy of Sciences (XDB22020200).